Fibonacciho postupnosť

Fibonacciho postupnosť je v skratke postupnosť čísel, v ktorej každý ďalší člen je súčtom dvoch predchádzajúcich členov. Samotná postupnosť sa začína číslami 0 a 1. Jednotlivé čísla tejto postupnosti potom nazývame Fibonacciho čísla. Táto postupnosť sa často nazýva aj zlatá cesta. Pomenovaná je podľa talianskeho matematika Leonarda z Pisy, ktorého nazývali Fibonacci.

Fibonacciho postupnosť vzorec

Fibonacciho čísla: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025,…

Fibonacciho postupnosť príklady

Medzi najznámejší príklad je určite ten s králikmi, pretože ho použil samotný Fibonacci. Na začiatku totiž máme samicu a samčeka králika. Pár je produktívny od druhého mesiaca života a každý mesiac splodí každý produktívny pár jeden ďalší pár. Pritom treba vždy prihliadať na to, že páry nikdy neumierajú a ani sa nezvyšuje počet potomkov.

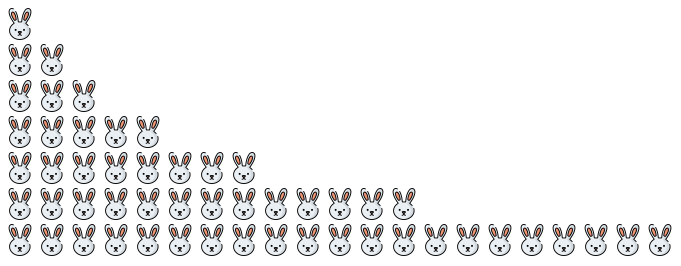
Fibonacciho postupnosť programovanie

Fibonacciho postupnosť sa využíva rovnako v prírode, či v programovaní. Podľa mnohých vedcov je základom všetkého a odráža sa v bežnom živote v rôznych oblastiach. Čo sa týka programovania je Fibonacciho postupnosť základom pre programovanie v rôznych jazykoch. Nazýva sa dynamické programovanie a má širokú oblasť využitia.

Zlatý rez

Zlatý rez je odvodený práve z Fibonacciho postupnosti. Výsledné pomery predchádzajúce a nadchádzajúceho čísla sa nachádzajú vždy v približnej hodnote 1,61803. Toto číslo je dôležité napríklad aj v geometrii pravidelných útvarov – pentagramov a pentagónov. V súčasnosti sa označuje aj ako číslo zlatého rezu – značka ϕ. Číslo 1,61803 je celkovo veľmi zaujímavé, napríklad mnohé proporcie v prírode majú blízko k tomuto číslu. Algebrický zápis:

ϕ = (1+√5)/2 = 1,6180339887…..